2. Das relationale Modell:

2.1. Theoretische Grundbegriffe:

Der Begriff der Relation kommt aus der Mengenlehre und stellt einen wesentlichen Begriff bei der Funktionsdefinition dar (eine Funktion ist eine Relation mit Nacheindeutigkeit). Dabei stellt eine Relation eine Menge geordneter Paare bzw. n-Tupel dar.

Eine Menge ist eine gedankliche Zusammenfassung irgendwelcher Objekte. Diese Objekte werden als Elemente der Menge bezeichnet. Mit <x,y> wird das geordnete Paar der Elemente x und y bezeichnet wobei gilt: <x1,y1> = <x2,y2> <-> x1 = x2 ^ y1=y2

Mit <x1,...,xn> wird das geordnete n-Tupel der Elemente x1,...,xn bezeichnet.

Eine zweistellige Relation X wird dann wie folgt definiert:

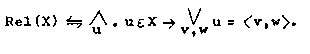
mit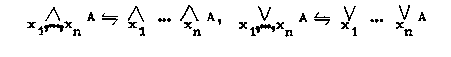
X ist eine Relation genau dann, wenn für jedes u gilt: Ist u in X, dann gibt es mindestens ein Element v und ein Element w derart, dass u gleich ist dem geordneten Paar <v,w>.)
Die Erweiterung auf mehrstellige Relationen sieht dann wie folgt aus:

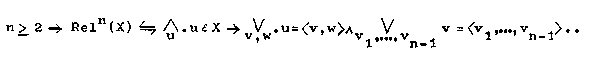
(X ist eine n-stellige Relation)

Wegen v = <v> gilt:

Das wichtige bei Relationen ist, dass alle Elemente einer Relation genau gleich viele Elemente im jeweiligen Tupel besitzen und dass jedes einzelne Element dieser Tupel aus der gleichen Menge genommen wird. Diese (Ausgangs-)Menge definiert somit den Typ, das sind alle möglichen Elemente, die an dieser Position des Tupel stehen können. Man sieht hier auch deutlich, warum bei einer Relation geordnete Tupel zum Einsatz kommen. Wäre das nicht der Fall, könnten also die Elemente im Tupel an beliebiger Stelle zu stehen kommen, würde es kaum Sinn machen die einzelnen Tupel aus verschiedenen Mengen zu belegen, da ja im fertigen Tupel keine direkte Beziehung zu den Elementen eines anderen Tupels aus der Menge der Relation hergestellt werden könnte.
Näheres zum Relationsbegriff und dessen logische Grundlagen finden sich unter anderem in TELEC & REP 1974.

2.2. Relationen und Datenbankmodelle:

Eine solche Relation kann nun vereinfacht als Tabelle dargestellt werden. Jedes Tupel bildet jeweils eine Reihe der Tabelle und die Spalten der Tabelle sind somit die Elemente des Tupels. Es kommen also Elemente gleichen Typs in einer solchen Aufstellung untereinander zu stehen, und jede Reihe der Tabelle hat definitionsgemäß gleich viele Spalten.
In der Nomenklatur der relationalen Datenbanken spricht man bei den Tupeln von Spalten bzw. Records, die Elemente des Tupels werden als Attribute bezeichnet und die Relation selbst, also die Sammlung der Tupel nennt man Tabelle.
Jedes Tupel kommt in einer Relation nur maximal einmal vor (es gibt keine Duplikate) und jedes Attribut enthält genau einen Wert (das kann auch ein "Null-Wert" sein).
Ein Attribut wiederum hat einen bestimmten Typ, der über die Menge der möglichen Werte, die sogenannte Domain, festgelegt wird. Es ist also bereits zum Zeitpunkt der Definition einer Relation bzw. Tabelle, also noch bevor konkrete Daten eingegeben werden, festgelegt welche Daten an welcher Stelle eingegeben werden können. Diese Mengen können unendlich sein (z.B. der Typ "Jahr"), aber auch aus nur zwei Elementen bestehen (z.B. der Typ "Status", mit den Werte "in Ordnung", "kaputt"). Ist der Typ eines Attributs einmal festgelegt, dann können an dieser Stelle der Relation nur mehr Elemente dieser Typ-Menge eingesetzt werden.
Es gibt ausserdem noch zusätzlich zur Definitionsmenge des Typs gewisse Operatoren, die sich auf Elemente dieses Typs anwenden lassen. Da diese einen Teil der Typdefinition darstellen müssen auch sie bereits vor Eingabe des ersten konkreten Datenwerts feststehen. So kann man z.B. auf Elemente des Typs "Jahr" die Operatoren "+", "-", "ist_ein_schaltjahr_?",..., anwenden, aber gewisse andere Operatoren wie z.B. "*" (Multiplikation) machen keinen Sinn und sind deshalb nicht möglich.
Natürlich werden diese so definierten Datentypen vom DBMS in Computer-System-Interne Datentypen umgewandelt wenn sie abgelegt werden. Das hat aber auf die Definition der Tabelle (bzw. Relation) keine wirklichen Auswirkungen. Jede Datenbank bietet ausserdem eine Reihe bereits vordefinierter Typen an, die der Einfachheit halber verwendet werden können ohne lange die Typmenge und die Typoperatoren definieren zu müssen (wie z.B. Integer, String, Float, Boolean, Datum, ..).
Zusätzlich zu den Typbeschränkungen gibt es auch noch "Integritätsbedingungen" die eine reine Typbeschränkung noch in sich weiter konkretisieren, also die Anzahl möglicher Elemente weiter einschränken, unterschiedliche Tupel oder Relationen untereinander mittels dieser Bedingungen verknüpfen. Integritätsbedingungen dienen somit der Gewährleistung der Integrität und Richtigkeit der Datenwerte in einer Datenbank.

Ein wesentlicher Aspekt des relationalen Modells ist, dass zusätzlich zu den eigentlichen Relationen, also den Tabellen mit den vordefinierten Attributen und konkreten Dateneinträgen, eine Übereinkunft bestehen muss, wie man dieses Gebilde und alle seine Elemente interpretieren muss. Man kann sagen, dass das relationale Modell die Syntax liefert, die Semantik muss aber vom Benutzer geliefert werden.

2.3. Relationale Algebra (Operatoren):

Operationen mit den Relationen manipuliert werden können, werden durch die Relationale Algebra festgelegt. Dabei ist nicht nur festgelegt wie man eine Relation manipuliert, sondern auch mehrere Relationen einer Datenbank miteinander verknüpfen kann. Dadurch wird erst eine Manipulation der Relationen ermöglicht. Diese relationalen Operatoren erfüllen das Prinzip der Abgeschlossenheit. D.h. das Ergebnis liefert immer eine Relation. Das erlaubt eine Schachtelung der relationalen Operatoren. Wesentlich im Hinblick auf das ontologische Modell ist in diesem Zusammenhang nur, dass es fix definierte logische Operatoren gibt um das logische, relationale, Grundgerüst umzuformen und in andere relationale Formen zu transformieren.

Die relationale Algebra erlaubt eine Reihe von Operationen die wesentlich für eine Datenbank sind wie z.B. die Abfrage, das Update, Integritätsbedingungen, und weitere Systemfunktionen wie Stabilitäts- und Sicherheitsfunktionalitäten.
Als Beispiel sollen hier nur die 8 Grundoperatoren nach E.F. Codd in Abbildung 2.1 dargestellt werden aus welchen sich weitere Operatoren durch Verschachtelung bilden lassen.

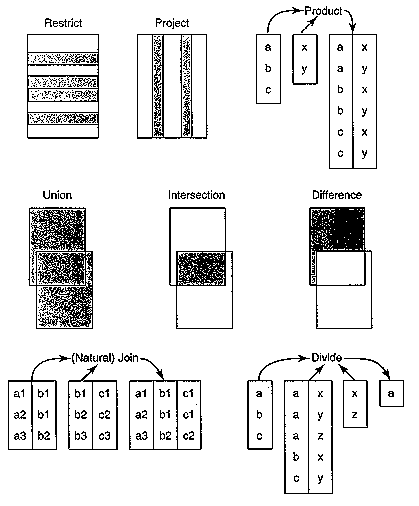
Abb. 2.1: Die 8 relationalen Grundoperatoren nach E.F. Codd im Überblick (aus DATE 2000).

Im Prinzip stellen diese Grundoperatoren nur einfache Erweiterungen von Mengen-Operatoren dar. Die Erweiterung beschränkt sich meist darauf, dass es sich eben nicht um Mengen, sondern um Relationen handelt, und dass um den Abschlussbedingungen zu genügen als Ergebnis aller Operatoren wieder eine Relation entstehen muss. Da bei der Konzeption der relationalen Operatoren, bzw. des relationalen Kalküls im Prinzip analoge Überlegungen zur Anwendung kommen wie bei der Konzeption der Kalküle der Aussagenlogik bzw. in weitere Folge der Prädikatenlogik erster Stufe sind die logischen Grundlagen dieser Konzepte die gleichen. Bei den relationalen Modellen hat man es im Gegensatz zu den traditionellen Logiken mit komplizierteren Datenstrukturen zu tun, also nicht mit einfachen Mengen, sondern eben mit Mengen von Tupeln. Diese relationale Erweiterung bringt zusätzlich Struktur in das Datenmodell und erlaubt so etwas wie Abbildungen, bzw. Zuordnungen zu konstruieren (analog dem Funktionsbegriff, der wiederum eine Erweiterung bzw. Spezialisierung der Relation darstellt).

Relationale Operatoren dienen allgemein gesehen einer Dynamisierung sonst statischer Dateninhalte. Durch Transformationen, also durch Anwendung der Operatoren der relationalen Algebra, lassen sich neue Strukturen in bestehenden Dateneinheiten erzeugen, was nicht nur zu einer anderen Sichtweise bestehender Fakten führen kann, sondern auch einer Erweiterung des Wissens darstellen kann. Im Folgenden soll in Ergänzung zu den oben aufgezeigten grafischen Darstellungen ein kurzer Überblick über die Semantik der wichtigsten relationalen Operatoren gegeben werden:

Vereinigung (Union):
Die "Vereinigung" zweier Relationen gleichen Typs bildet eine Relation (gleichen Typs wie die Ausgangsrelationen), welche aus Tupeln besteht, die entweder in einer oder in beiden der Ausgangsrelationen vorkommen.

Schnitt (Intersect):
Der "Schnitt" zweier Relationen A, B (gleichen Typs) liefert eine neue Relation (ebenfalls gleichen Typs) mit Tupeln, die sowohl in Relation A als auch in Relation B vorkommen. (Falls kein Tupel in A und B gleichzeitig vorkommt, kann das auch die Null-Relation sein.)

Differenz (Difference):
Die Differenz zweier Relationen gleichen Typs A und B (kurz A minus B) liefert eine Relation gleichen Typs, in der alle Tupel der Relation A enthalten sind, die nicht in B vorkommen.

Kartesisches Produkt (Product):
Man spricht hier auch vom Kartesischen Produkt zweier (unterschiedlicher) Relationen. Wenn man das mengentheoretische Kartesische Produkt anwenden würde, ergäbe das geordnete Paare von Tupeln. Da aber die Abgeschlossenheit erhalten werden soll muss es zu einer Erweiterung kommen. Das kartesische Produkt zweier Relationen A, B (kurz A mal B) ohne gleiche Attribute ist deshalb eine neue Relation mit allen Attributen, also der mengentheoretischen Vereinigung der Attribute, der Relationen A und B und Tupeln die aus der mengentheoretischen Vereinigung aller Tupel aus A und B entstehen. Die Anzahl der Attribute der neuen Relation ist die Summe der Anzahl der Attribute der Relationen A und B. Die Anzahl der Tupel der neuen Relation ist gleich der Anzahl der Tupel in Relation A mal der Anzahl der Tupel in Relation B.

Beschränkung (Restrict):
Bei der Beschränkung benötigt man eine (Beschränkungs-)Bedingung welche auf die Tupel einer Relation anwendbar ist (z.B. <, >, =) und wahrheitsfunktional eine Klassifikation (wahr, falsch) der Tupel ermöglicht. Die Tupel die mit dem Wahrheitswert "wahr" klassifiziert werden gehören zur neuen Ergebnisrelation und bilden so eine Auswahl der ursprünglichen Tupel.

Projektion (Project):
Die Projektion einer Relation mit den Attributen A1,...Ax ergibt eine neue Relation mit den Attributen A1,..,Ay, wobei diese Attribute eine Teilmenge der Attribute der Ausgangsrelation darstellen. Die Tupel der Ergebnisrelation sind die gleichen wie die der Ausgangsrelation, reduziert um die Werte der nicht mehr vorhandenen Attribute.

Verknüpfung (Join):
Bei der "natürlichen" Verknüpfung ("natural join"), oder kurz nur Verknüpfung, handelt es sich um die Verbindung zweier Relationen mit teilweise gleichen Attributen. Hat die Relation A die Attribute {X1,..,Xm, Y1,..,Yn} und die Relation B die Attribute {Y1,..Yn, Z1,..,Zp} so kann mit dem Verknüpfungsoperator über ein oder mehrere gleiche Attribute {Y1,..,Yn} eine Verknüpfung der beiden Relationen erreicht werden. Die neue Relation enthält dann die Attribute {X1,..,Xm, Y1,..,Yn, Z1,..,Zp} mit den Tupeln mit Werten aus den Tupeln der Relationen A für die Attribute {X1,..,Xm, Y1,..,Yn} und Werten aus der relation B für die Attribute {Y1,..Yn, Z1,..,Zp}. Somit müssen die Werte der Attribute {Y1,..,Yn} gleich sein um eine solche Konstellation zu ermöglichen.
Es kann aber auch eine Bedingung (z.B. >, <,...) verwendet, die auf gleiche Attribute angewendet wird um die Verknüpfung der Relationen nicht nur über die Gleichheit der Werte der gleichen Attribute zu definieren, sondern eben über eine Bedingung. Diese Art der Verknüpfung wird dann "bedingte" Verknüpfung ("conditional join") genannt.

Division (Divide):
Zur Division benötigt man 3 Ausgangsrelationen: die Dividenden- (A), den Divisor- (B) und den Mediator-Relation (C). Die Dividenden- und Divisor-Relation haben dabei disjunkte Attribute-Mengen und die Mediator-Relation hat als Attribute-Menge die Vereinigung der Attribute-Mengen von Dividenden- und Divisor-Relation. Man spricht von der Division von A durch B mittel C. Die Ergebnisrelation hat dann als Attribute die Attribute der Dividenden-Relation A, und die Tupel setzen sich aus den Werten zusammen, wo die Werte eines Tupels der Relation C für gleiche Attribute gleiche Werte in den Tupeln der Relationen A und B haben.

Zusätzlich zu den oben genannten Grundoperatoren finden sich in modernen Datenbanksystemen meist noch folgende Operatoren als Erweiterung: Rename, Semijoin, Semiminus, Extend, Summarize, Tclose, Group, Ungroup. Diese sollen aber hier nicht weiter behandelt werden.

Die Syntax der relationalen Operatoren ist in diesem Zusammenhang irrelevant. Es soll nur erwähnt werden, dass diese Syntax das Grundgerüst der meisten relationalen Datenbanksprachen bildet. Es muss aber gesagt werden, dass z.B. für SQL (Structured Query Language) nur teilweise die relationale Algebra zum Einsatz kommt, aber auch der wesentlich deskriptivere relationale Kalkül. Mittels der relationalen Algebra wird beschrieben, welche Operationen durchgeführt werden müssen um zu einem bestimmten Ergebnis zu kommen. Beim relationalen Kalkül wird spezifiziert was das Ergebnis sein soll, ohne auf die Spezifika der einzelnen Operatoren einzugehen (die Auswahl der Operatoren wird dann dem DBMS überlassen, welches dann mittels Optimierungsalgorithmen die günstigsten Operatoren finden sollte). Relationale Algebra und der relationale Kalkül sind aber logisch äquivalent. D.h. alle Formulierungen des relationalen Kalküls lassen sich in äquivalente Formulierungen der relationalen Algebra übersetzen und umgekehrt. Man könnte in Analogie zu den Logikkalkülen der Aussagen- und Prädikatenlogik von einer deduktiven Hülle sprechen, die sich mittels des relationalen Kalküls, also auch mittels der relationalen Algebra und deren Operatoren, bilden läßt.
Näheres zu dieser Thematik in DATE 2000.

2.4. Optimierung relationaler Modelle:

Ziel dieses Konstrukts des relationalen Modells ist es, aufgrund der Struktur eine optimierte Form der Modellierung zu finden, sodass die Abbildung konsistent, in sich geschlossen und widerspruchsfrei ist. Es soll weiters keinerlei Redundanzen geben, was wesentlich die Integrität der Daten erhöht. Ausserdem sollte eine dem Problem angemessene Atomisierung der Attribute stattfinden. Darunter versteht man, dass die in den Attributen abgelegten Daten, in Hinblick auf die Problembeschreibung, möglichst elementare Dinge oder Eigenschaften darstellen, die nicht weiter zerlegt werden können (sollen). Da die relationalen Operatoren maximal auf einzelne Attribute als kleinst mögliche Teile zugreifen können (bzw. eine Relation mit einem einzigen Attribut) ist es notwendig diese Attribute so zu gestalten, dass darin implizit enthalten keine Information versteckt ist, auf die man zu einem späteren Zeitpunkt zugreifen möchte. Um zu einer optimierten Modellierung zu kommen gibt es einerseits gewisse Analyseverfahren (z.B. Entity-Relationship, siehe oben) und andererseits die sogenannten Normalisierunsgregeln. Diese dienen dazu beliebige Relationen gemäß obigen Prinzipien zu optimieren, also z.B. Redundanzen auszumerzen.

Eine Erweiterung des "einfachen" relationalen Modells stellen objekt-relationale Modelle (siehe unten) und mehrdimensionale relationale Modelle dar. Bei letzterem werden als Elemente der Tupel wieder Tupel, und als Elemente dieser Tupel wiederum Tupel, usw. verwendet. Das führt dazu, dass einige Grundsätze der Normalisierung nicht mehr anwendbar sind, da ja nun ein Element einer Relation aus mehreren Einheiten bestehen kann. Sinnvoll ist dieser Ansatz besonders dort, wo die mehrdimensionale Struktur der Relation eine Entsprechung in der Struktur der Daten findet. So kann z.B. der Ort in einem Lagerraum sehr einfach und direkt in eine dreidimensionale relationale Struktur übersetzt werden. Da sich aber keine wesentlichen Änderungen für die Prinzipien des relationalen Modells ergeben, soll diese Erweiterung hier nicht näher besprochen werden.

©Mag.Dr. Alfred Hofstadler : "Datenbanken und Wittgenstein: ontologische Vergleiche",Diplomarbeit an der Universität Wien, März 2001.